Graphs of equations in polar coordinates
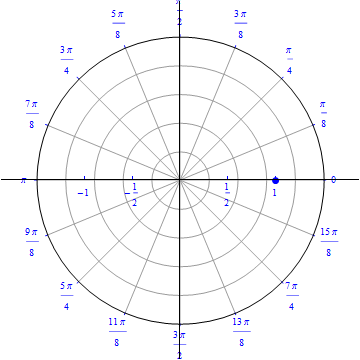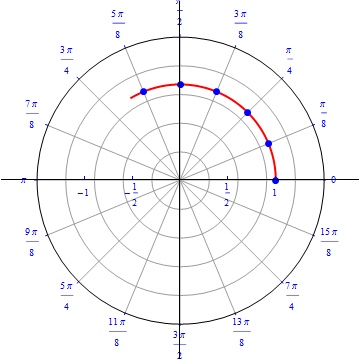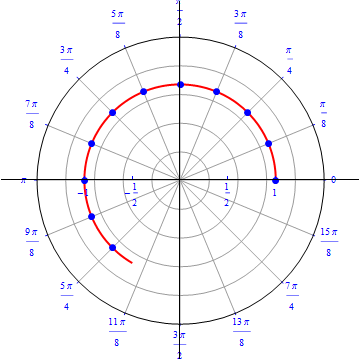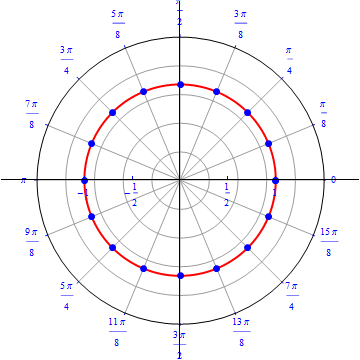
Example 1: A circle of radius 1, centered on the origin.
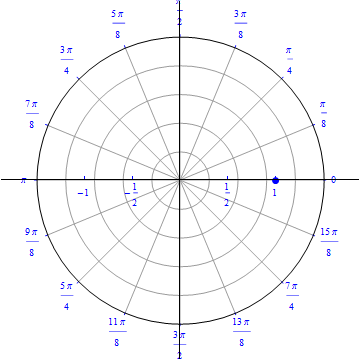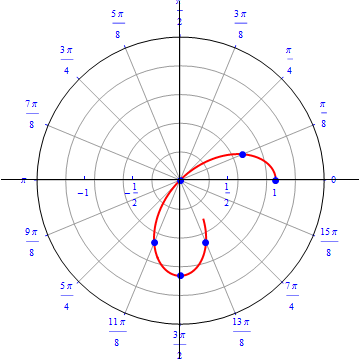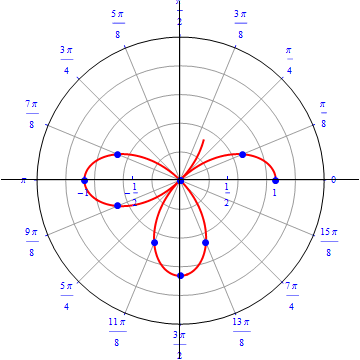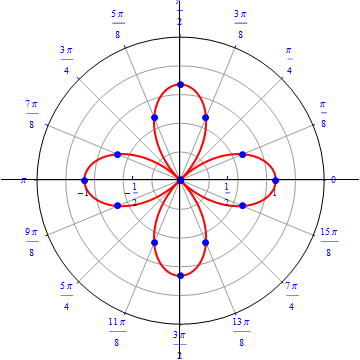
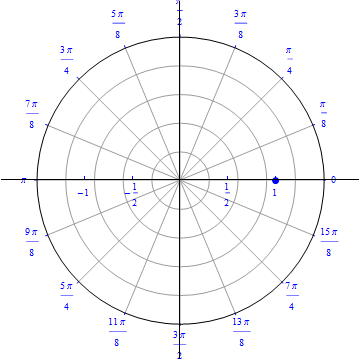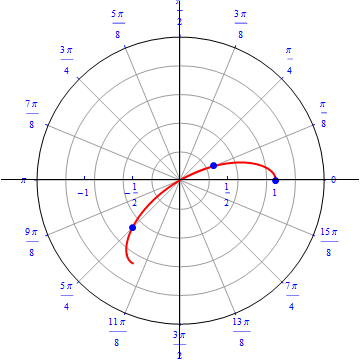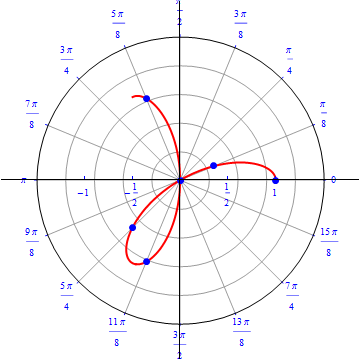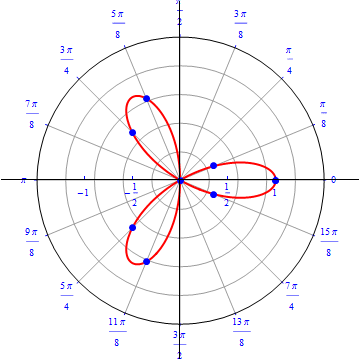
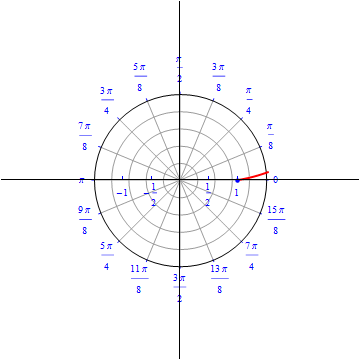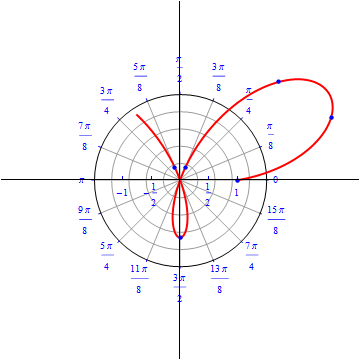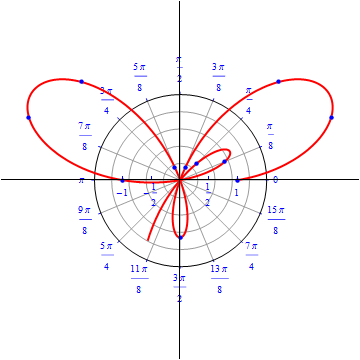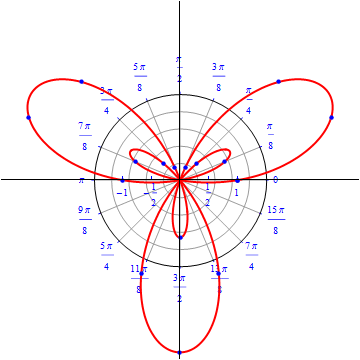
This is the the graph of the equation $r(\theta)=1, 0\leq \theta \leq 2 \pi.$
Example 2: Circles with center outside the origin.
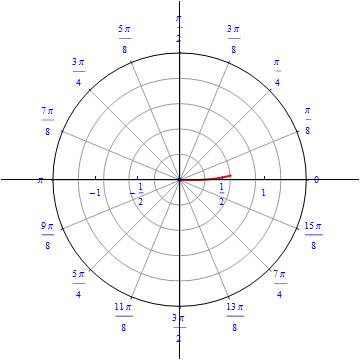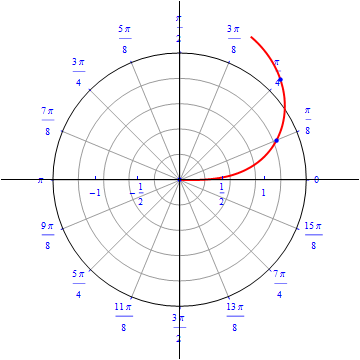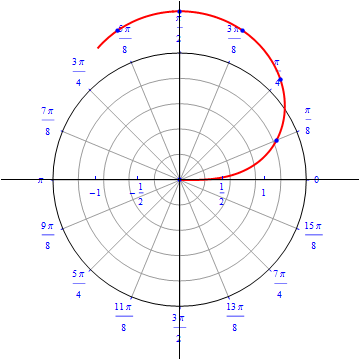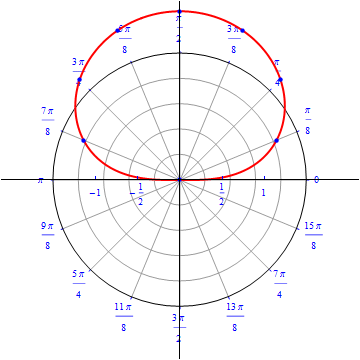
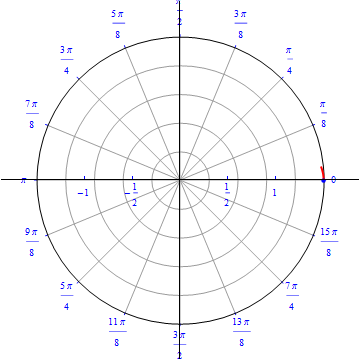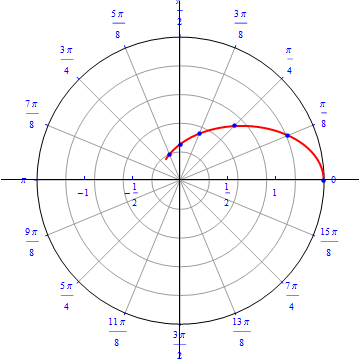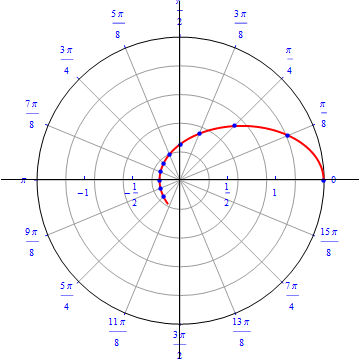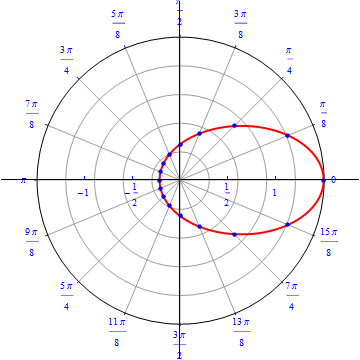
The graph of $r(\theta) = cos (\theta), 0\leq \theta \leq \pi.$ 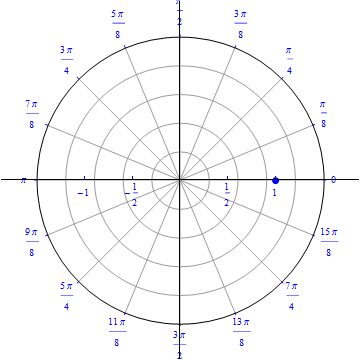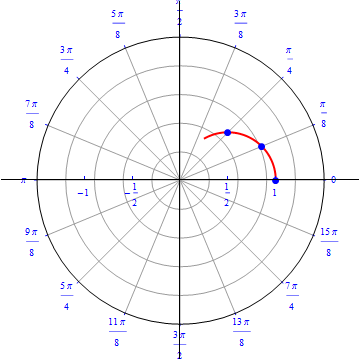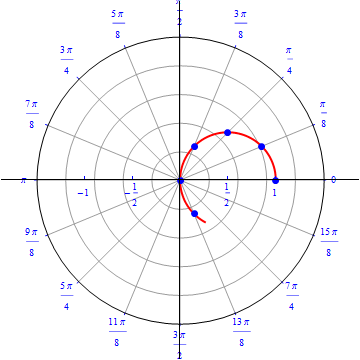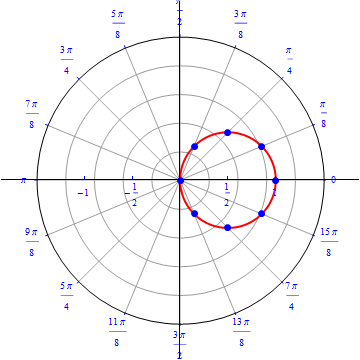 |
The graph of $r(\theta) =- cos (\theta), 0\leq \theta \leq \pi.$ 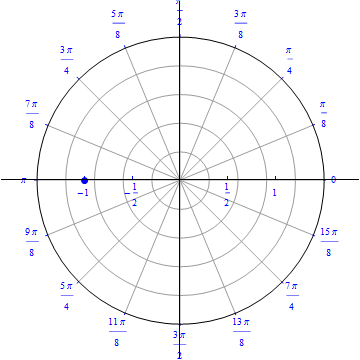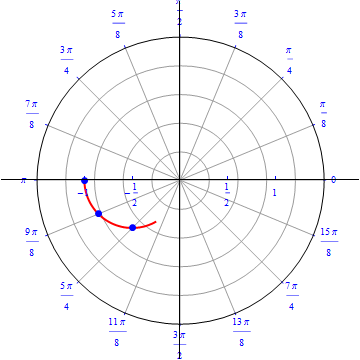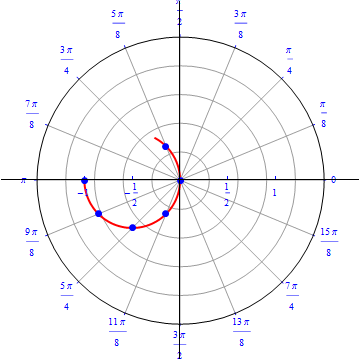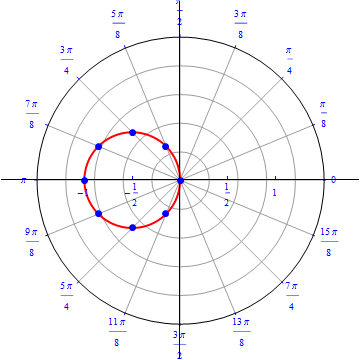 |
The graph of $r(\theta) = sin (\theta), 0\leq \theta \leq \pi.$ 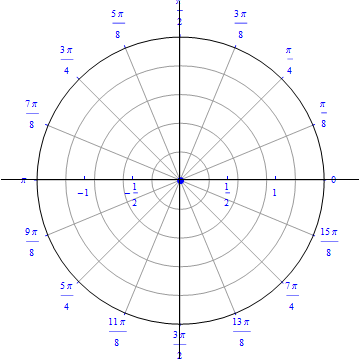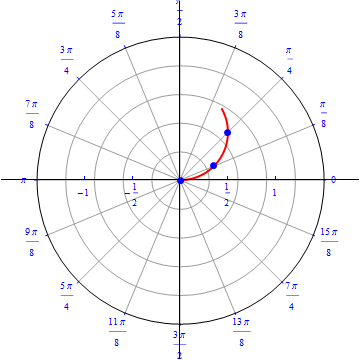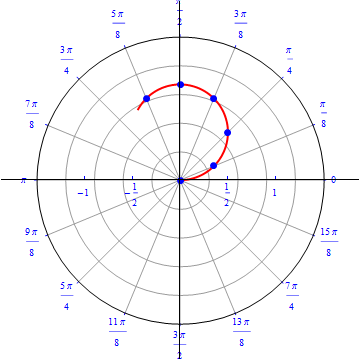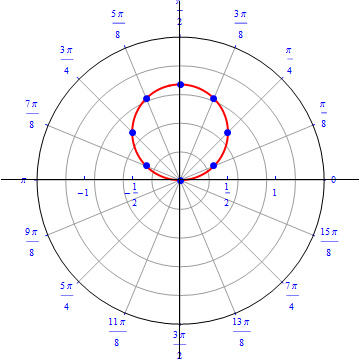 |
The graph of $r(\theta) = - sin (\theta), 0\leq \theta \leq \pi.$ 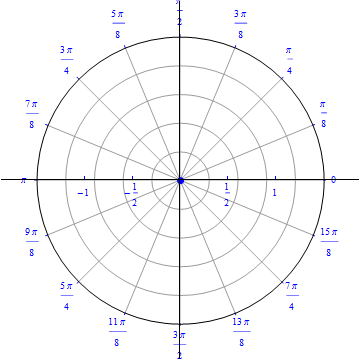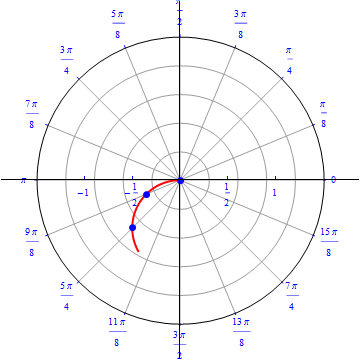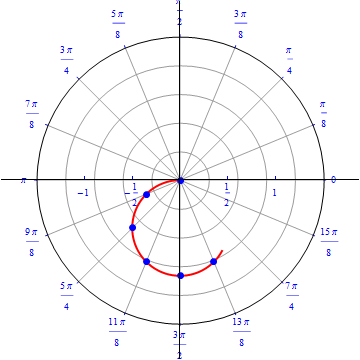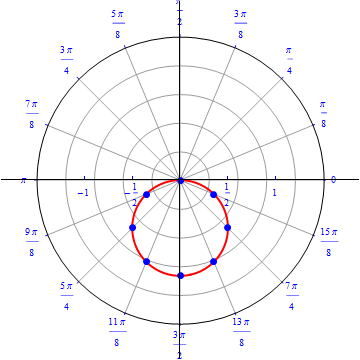 |
Example 3: A flower with four petals.
\begin{equation} r(\theta) = cos\, (2 \,\theta), \,\,\,\,\, 0\leq \theta \leq 2\,\pi . \end{equation}
The graph of $r(\theta) = cos (2 \theta).$
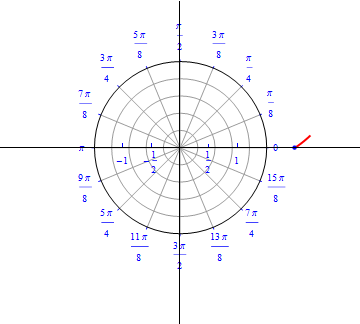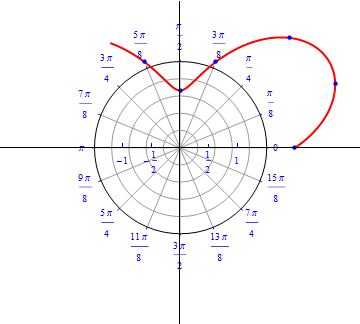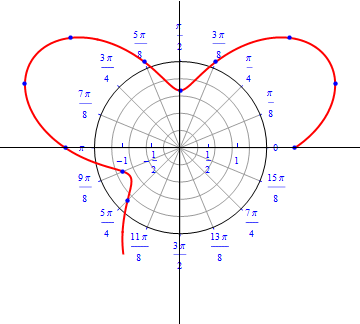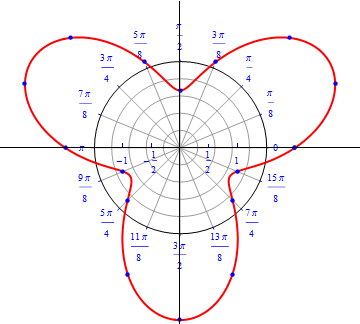
Example 4: A flower with three petals.
\begin{equation} r(\theta) = cos\,( 3 \,\theta), \,\,\,\,\, 0\leq \theta \leq \,\pi . \end{equation}
The graph of $r(\theta) = cos (3 \theta).$
Example 5: Cardioids .
The graph of $r(\theta) = 1+ cos (\theta), 0\leq \theta \leq 2\pi.$ 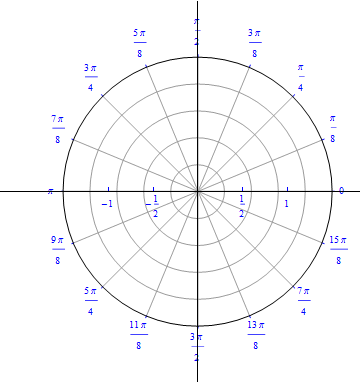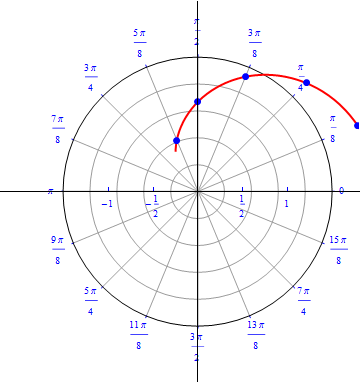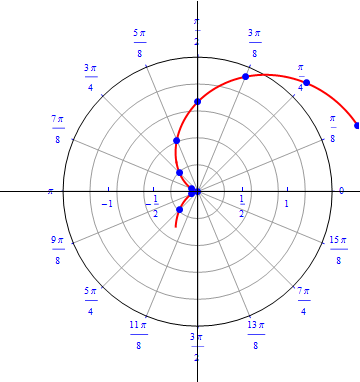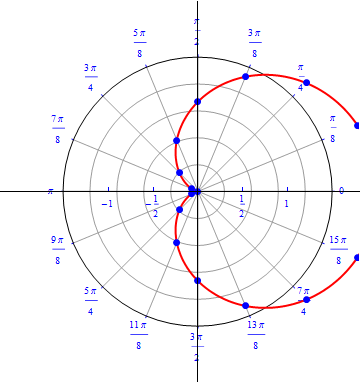 |
The graph of $r(\theta) =1 - cos (\theta), 0\leq \theta \leq 2\pi.$ 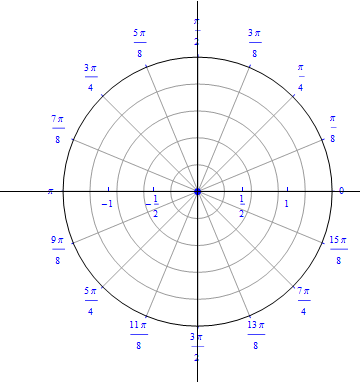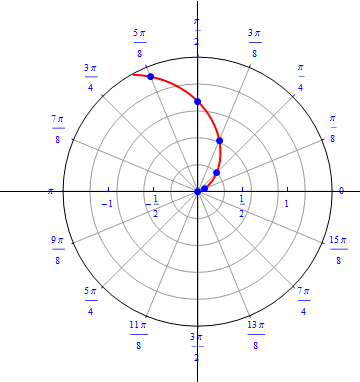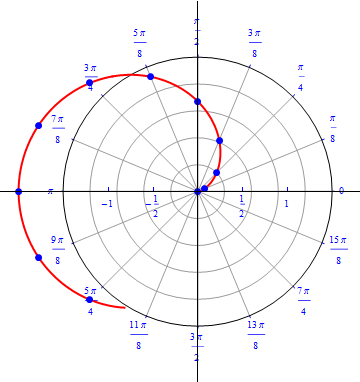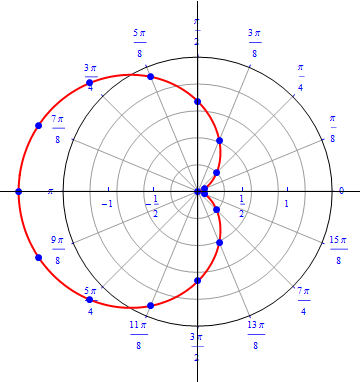 |
The graph of $r(\theta) = 1 + sin (\theta), 0\leq \theta \leq 2\pi.$ 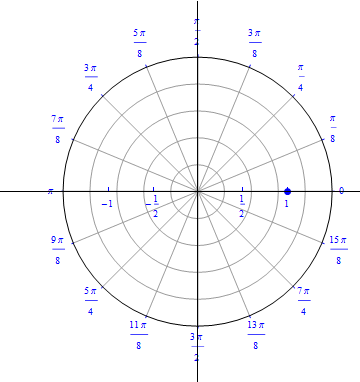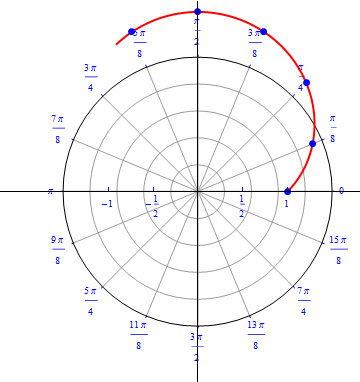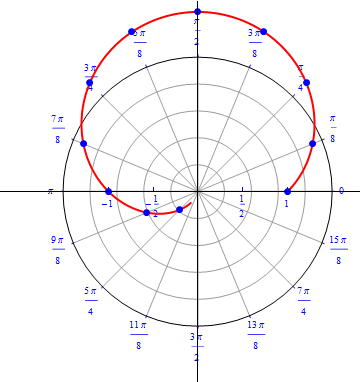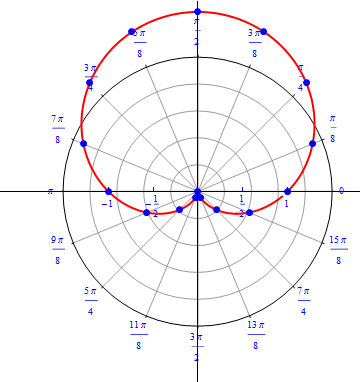 |
The graph of $r(\theta) = 1 - sin (\theta), 0\leq \theta \leq 2 \pi.$ 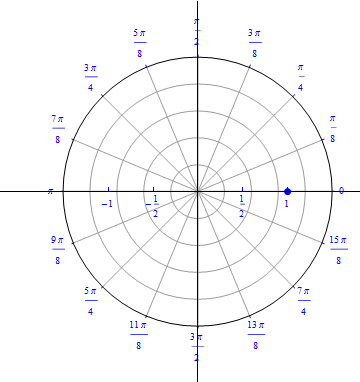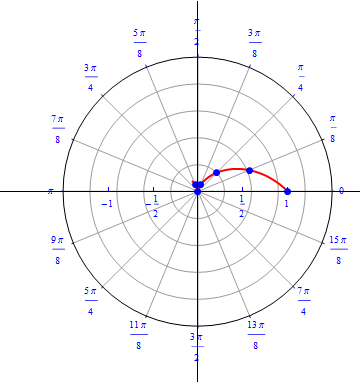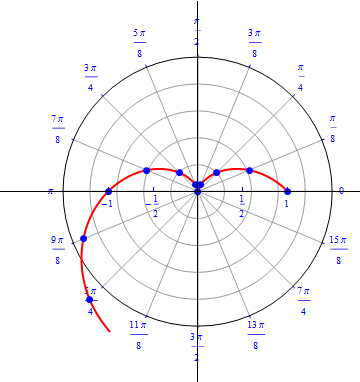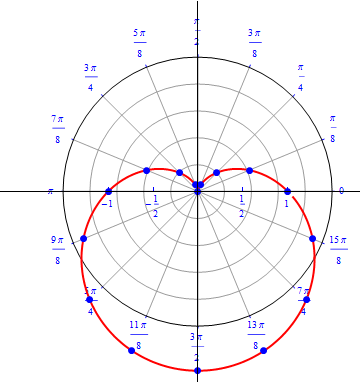 |
Example 6: Limaçon .
The graph of $r(\theta) = \cos (\theta), 0\leq \theta \leq \pi.$ 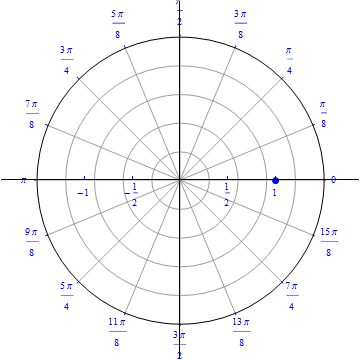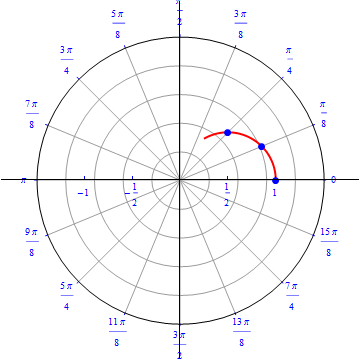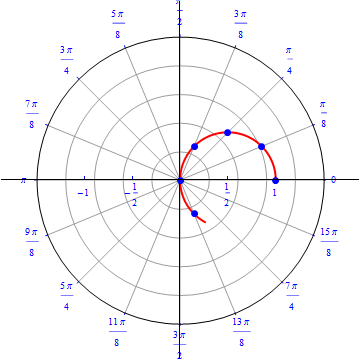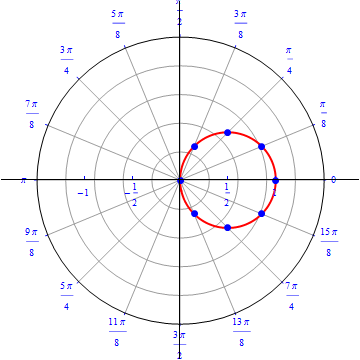 |
The graph of $r(\theta) =0.5+ \cos (\theta), 0\leq \theta \leq 2\pi.$ 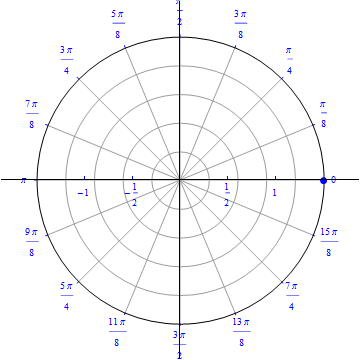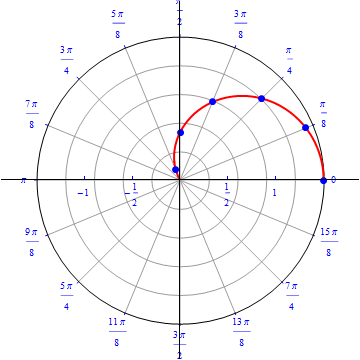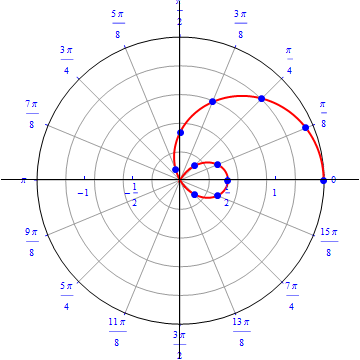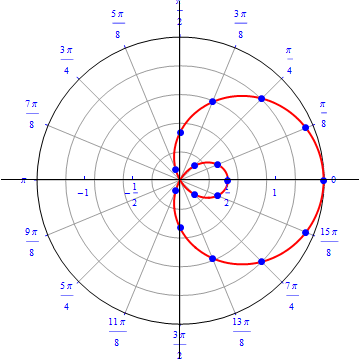 |
The graph of $r(\theta) = 1 + \cos (\theta), 0\leq \theta \leq 2\pi.$ 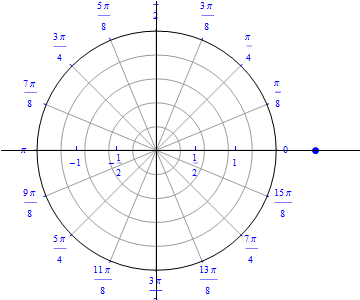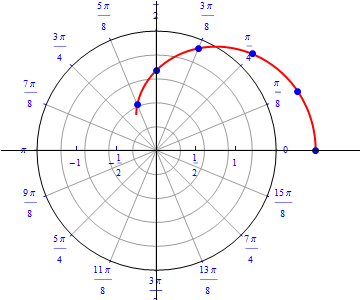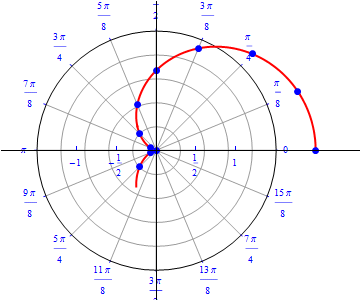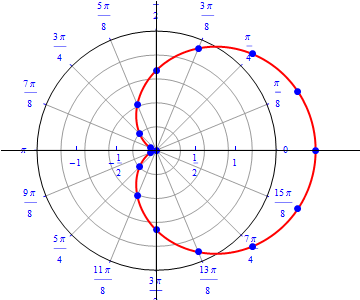 |
The graph of $r(\theta) = 1.5 + \cos (\theta), 0\leq \theta \leq 2 \pi.$ 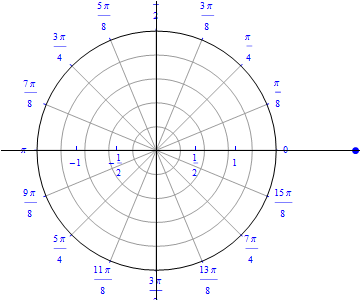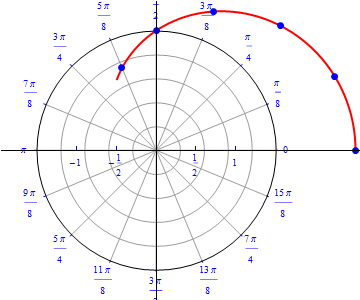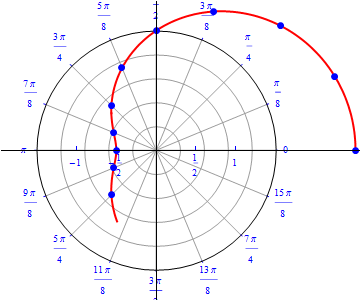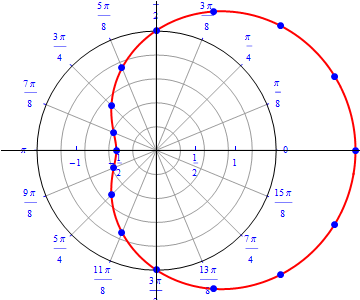 |
Example 7:A spiral.
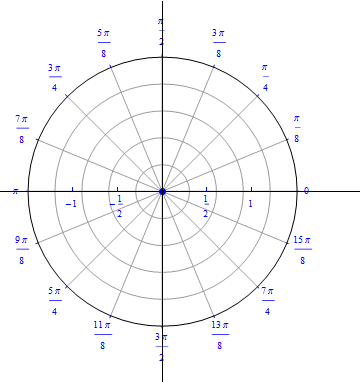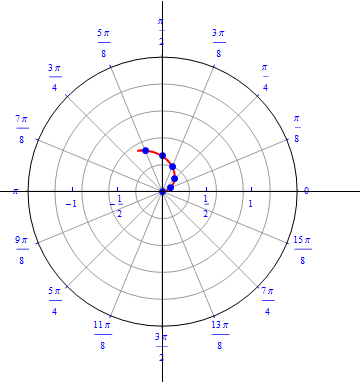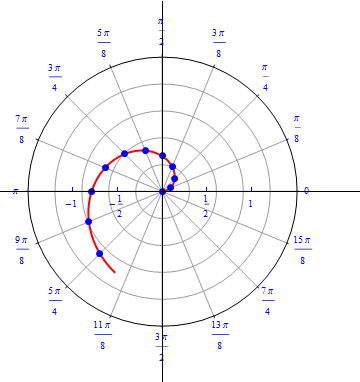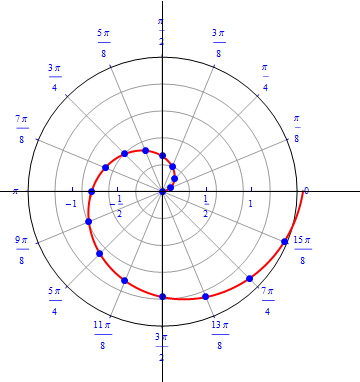
\begin{equation} r(\theta) = \theta / 4, \,\,\,\,\, 0\leq \theta \leq \, 2\,\pi . \end{equation}
The graph of $r(\theta) = \theta / 4.$
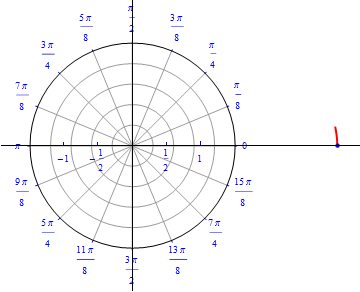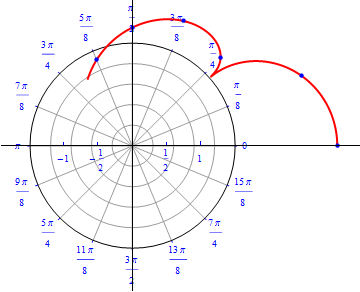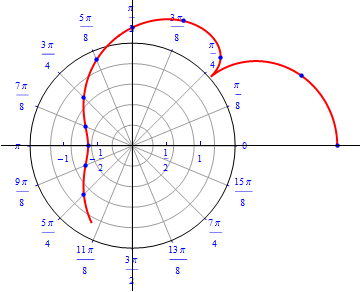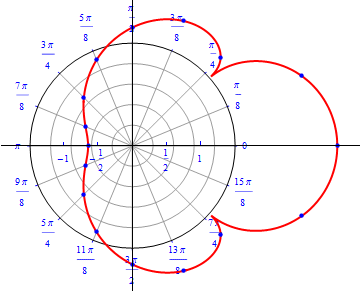
Example 8: A lettuce
\begin{equation} r(\theta) = 2 Cos(\theta) + |4 Cos(\theta)-3| \,\,\,\,\, 0\leq \theta \leq \, 2\,\pi . \end{equation}
The graph of $r(\theta) = 2 Cos(\theta) + |4 Cos(\theta)-3|.$
Example 9: An ellipse .
\begin{equation} r(\theta) = 1.5/(4- 3 \cos(\theta)) \,\,\,\,\, 0\leq \theta \leq \, 2\,\pi. \end{equation}
The graph of $r(\theta) = 1.5/(4- 3 \cos(\theta)).$
Example 10: A hippopede .
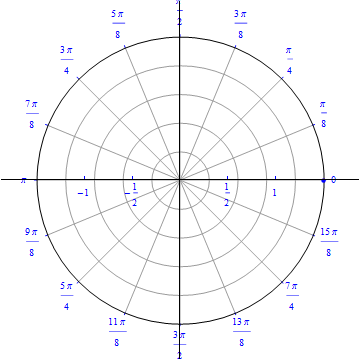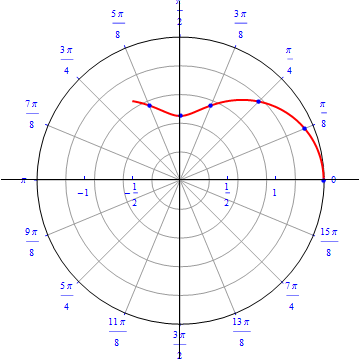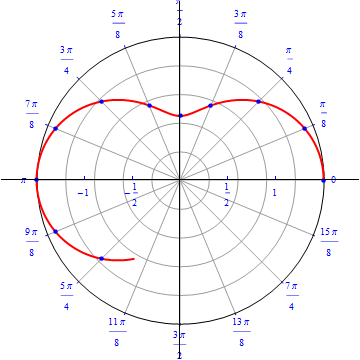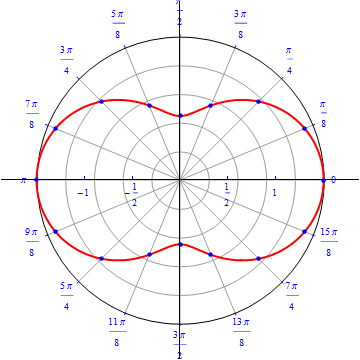
\begin{equation} r(\theta) = 1.5\sqrt{1-0.8(\sin(\theta))^2} \,\,\,\,\, 0\leq \theta \leq \, 2\,\pi . \end{equation}
The graph of $r(\theta) = 1.5\sqrt{1-0.8(\sin(\theta))^2}.$
Example 11: A rabbit ears.
\begin{equation} r(\theta) = 1/2 e^{\sin(\theta)-2 \cos(4 \theta)} \,\,\,\,\, 0\leq \theta \leq \, 2\,\pi . \end{equation}
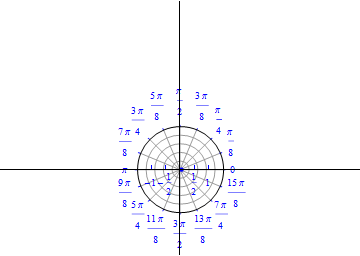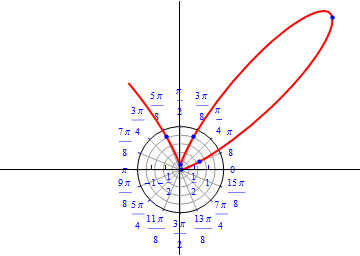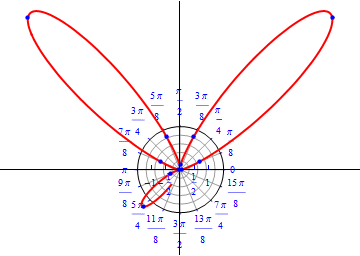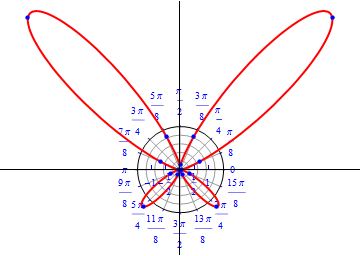
The graph of $r(\theta) = 1/2 e^{\sin(\theta)-2 \cos(4 \theta)} .$
Example 12: Inner-loop limaçon
The graph of $r(\theta) = 1+ 2 \cos (\theta), 0\leq \theta \leq 2\pi.$ 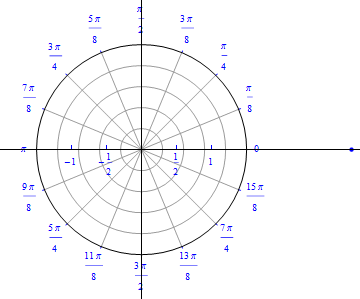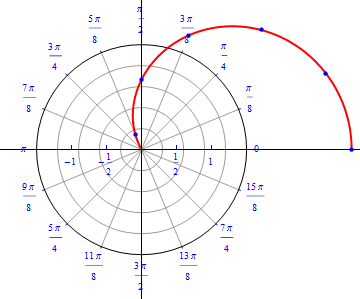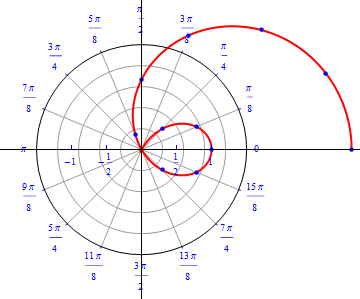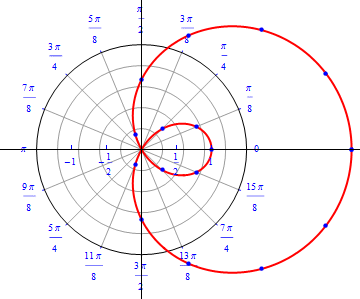 |
The graph of $r(\theta) =1- 2 \cos (\theta), 0\leq \theta \leq 2\pi.$ 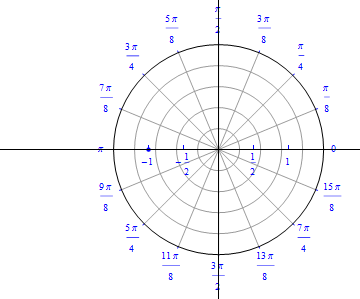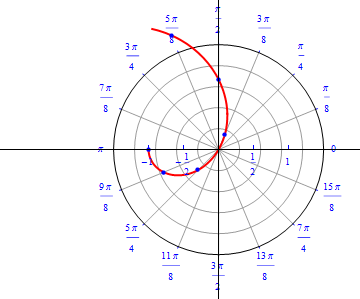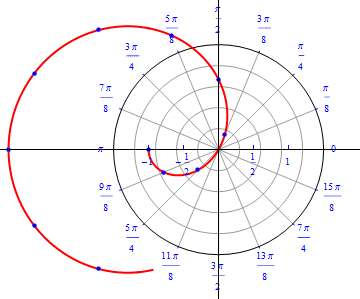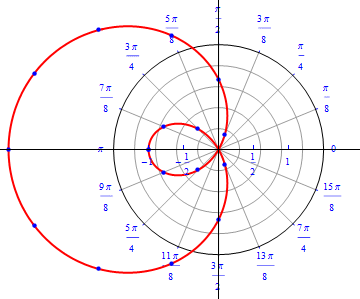 |
The graph of $r(\theta) = 1 + 2 \sin (\theta), 0\leq \theta \leq 2\pi.$ 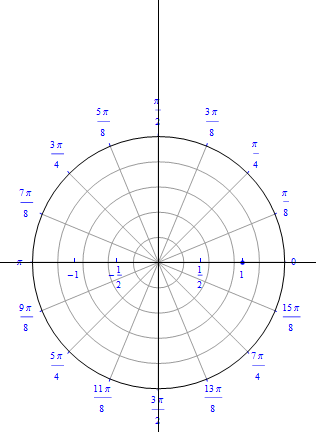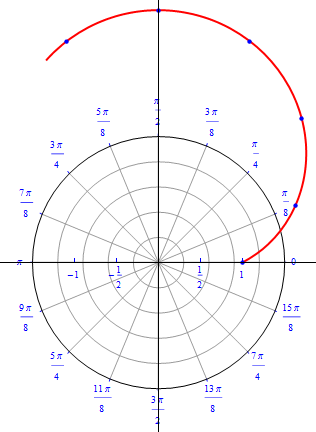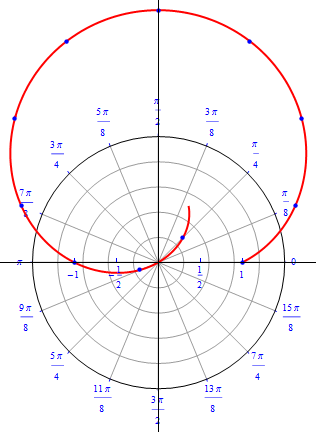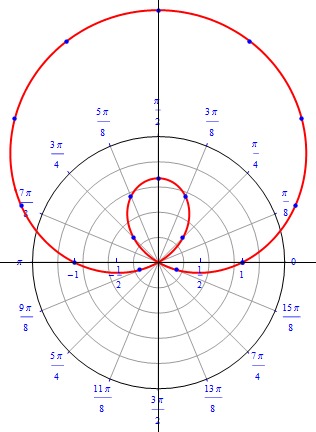 |
The graph of $r(\theta) = 1 - 2\sin (\theta), 0\leq \theta \leq 2 \pi.$ 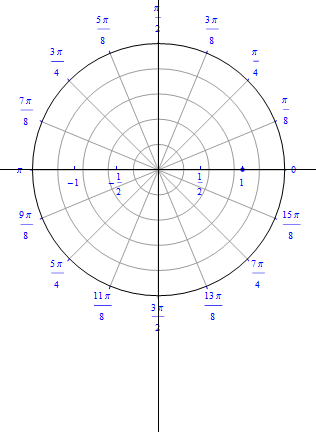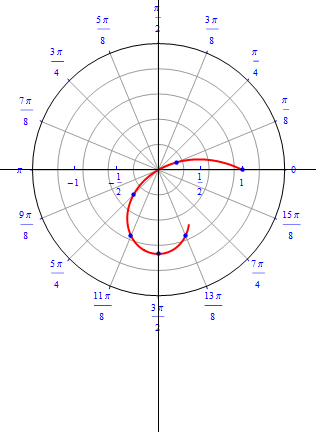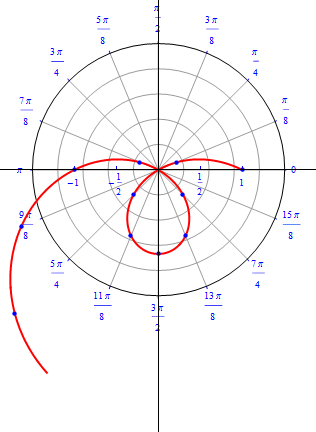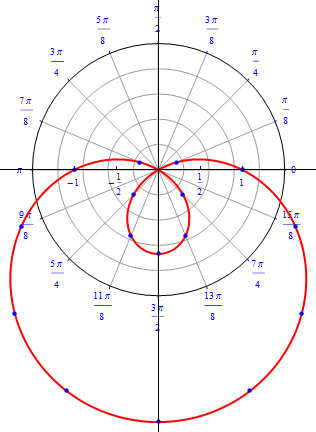 |
Example 13:
\begin{equation} r(\theta) = 1+ 2 \sin (2 \theta)\,\,\,\,\, 0\leq \theta \leq \, 2\,\pi. \end{equation}
The graph of $r(\theta) = 1+ 2 \sin (2 \theta) .$
Example 14:
\begin{equation} r(\theta) = 2+ \sin (3 \theta)\,\,\,\,\, 0\leq \theta \leq \, 2\,\pi . \end{equation}
The graph of $r(\theta) = 2+ \sin (3 \theta) .$
Example 15: Lemniscates .
The graph of $r(\theta) = \sqrt{ 4 \cos (2\theta)}, 0\leq \theta \leq 2\pi.$ 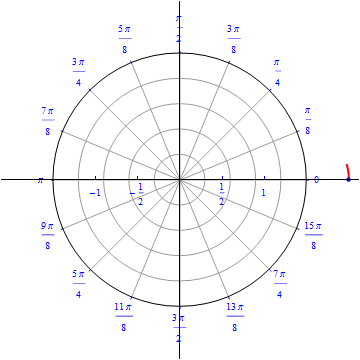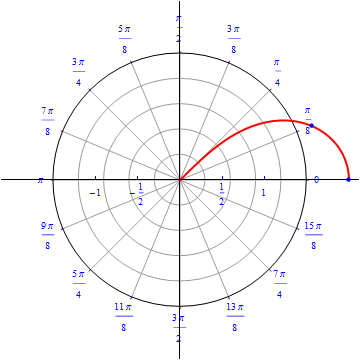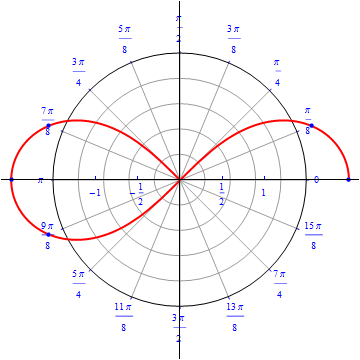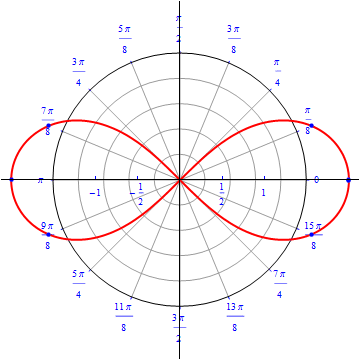 |
The graph of $r(\theta) =\sqrt{ - 4 \cos (2\theta)}, 0\leq \theta \leq 2\pi.$ 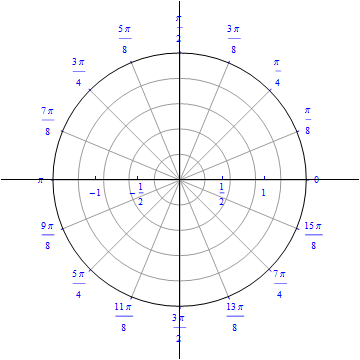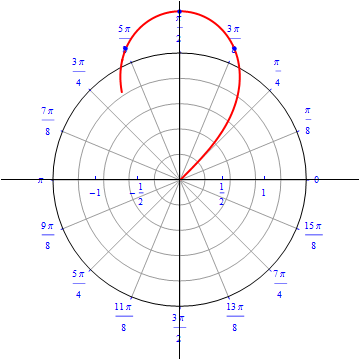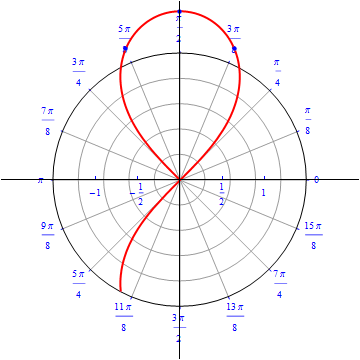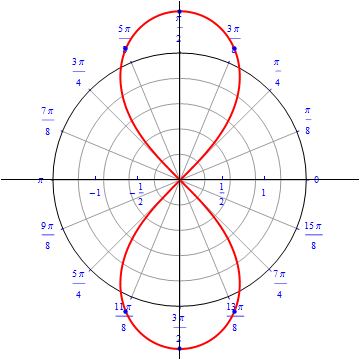 |
The graph of $r(\theta) = \sqrt{ 4 \sin (2\theta)}, 0\leq \theta \leq 2\pi.$ 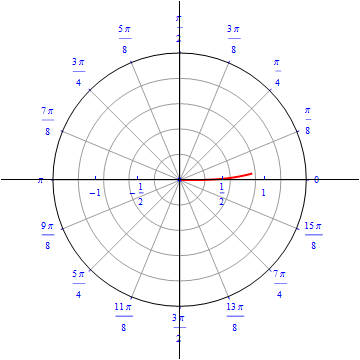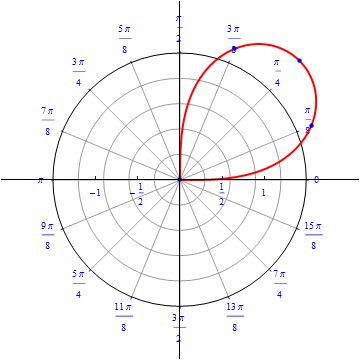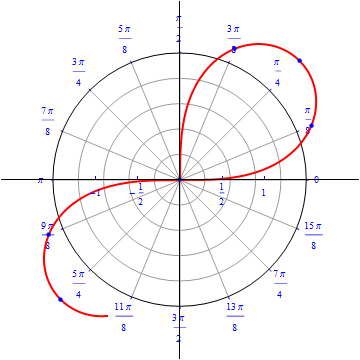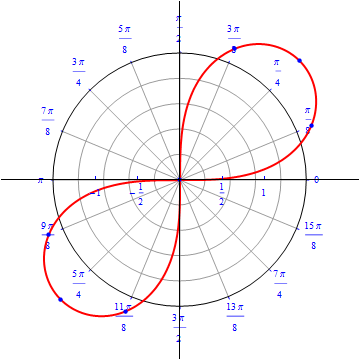 |
The graph of $r(\theta) = \sqrt{ - 4 \sin (2\theta)}, 0\leq \theta \leq 2 \pi.$ 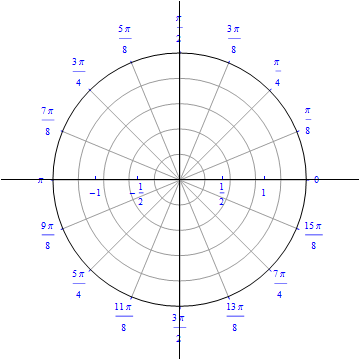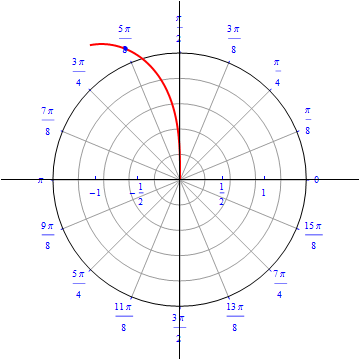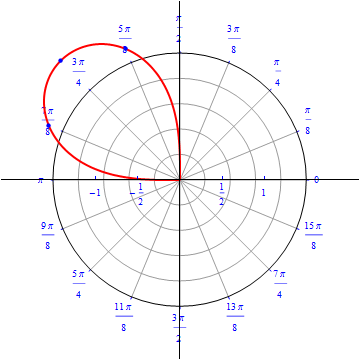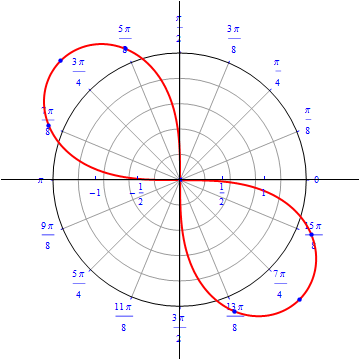 |
\begin{equation} r(\theta) = \sqrt{4 \sin ( \theta)},\,\,\,\, 0\leq \theta \leq \, 2\,\pi . \end{equation}
The graph of $r(\theta) = \sqrt{4 \sin ( \theta)} .$